
Механики XXI веку. № 16 2017 г.
296
ваемой как в аналитическом выражении, так и в графическом отображении своих частотных
характеристик, и одновременно представительно отражала основные свойства колебательной
системы автомобиля в целом. Такой динамической системой, формирующей независимые
вертикальные колебания на рессорах и шинах передней или задней частей автомобиля, явля-
ется система, эквивалентная подвеске. Эта система постоянно используется для расчетов ко-
лебаний, плавности хода и нагруженности элементов ходовой части автомобиля, а также при
проектировании и расчете конструкции самой подвески. И только после всестороннего ис-
следования модели на примере подобной колебательной системы, и уяснения влияния вно-
симого ею эффекта сглаживающей способности шины на результаты расчетов можно вво-
дить новую модель в математическое описание эквивалентных систем автомобиля любого
порядка сложности для их решения и анализа.
Построение математической модели подвески с учетом эффекта переменного
сглаживания шины.
Построение функциональной схемы колебательной системы, эквива-
лентной подвеске автомобиля, учитывающей особенности новой модели сглаживающей спо-
собности шины, и составление уравнений движения ее масс будем основывать на следующих
допущениях:
1) скорость качения колеса по дороге принимается постоянной;
2) поверхность дороги считается абсолютно жесткой;
3) колебания неподрессоренных масс в вертикальной плоскости не ведут к потере
контакта шины с опорной поверхностью дороги;
4) характеристики воздействия микропрофиля неровной дороги на колеса левого и
правого борта автомобиля принимаются одинаковыми;
5) колебания подрессоренных масс передней и задней частей автомобиля считаются
независимыми;
6) динамическая система, эквивалентная подвеске, представляется двумя сосредото-
ченными массами с упругими и диссипативными связями между собой, которые перемеща-
ются в вертикальной продольной плоскости. Кроме того, сюда необходимо включить допу-
щения, отражающие новую модель сглаживающего эффекта шины, а именно:
7) пневматическая шина обладает свойствами сосредоточенного упруго-
демпфирующего элемента с коэффициентами нормальной жесткости и поглощения энергий
вертикальных колебаний;
8) пневматическая шина моделируется тонкой, идеально эластичной оболочкой, кото-
рая плотно облегает все неровности в зоне контакта;
9) длина пятна контакта шины определяется параметрами эквивалентной колебатель-
ной системы и непрерывно изменяется в процессе перемещения ее масс.
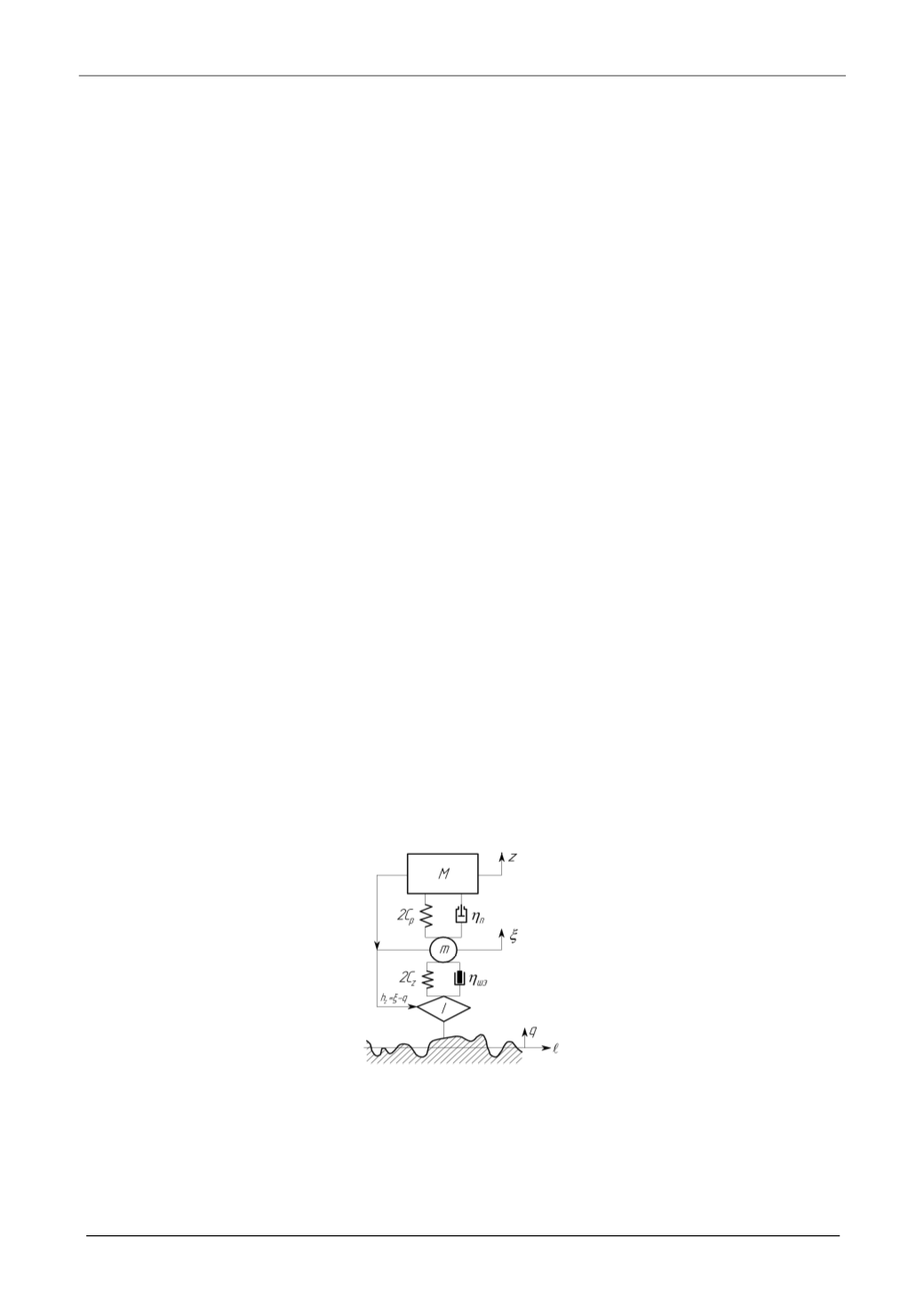
Рис. 1. Функциональная схема колебательной системы, эквивалентной подвеске автомобиля, с учетом
поглощающей и сглаживающей способности шин:
М
– приведенная подрессоренная масса, приходящаяся на подвеску; 2
С
р
– суммарный коэффициент нормальной же-
сткости упругих элементов подвески;
n
– коэффициент суммарного сопротивления в подвеске;
m
– неподрессорен-
ная масса; 2
С
z
– суммарный коэффициент нормальной жесткости шин;
шэ
– эквивалентный коэффициент вязкого
сопротивления в шинах;
Н
ш
,
n
– параметры эллиптическо-степенной модели;
z
,
– вертикальные перемещения под-
рессоренной и неподрессоренной масс;
q
– текущее значение ординат микропрофиля поверхности дороги под осью
колес;
J
– звено сглаживания
















